
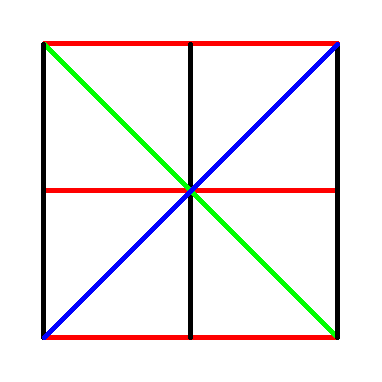
Below we see the type B2 (or C2) Steinberg torus. It is formed by identifying opposite sides of a square that has been cut into eight right triangles corresponding to the signed permutations of {1,2}.
This region is also the union of the (closure of the) alcoves neighboring the origin in affine B2 (or C2). (It is also worth noting that this is the barycentric subdivision of the square.)

