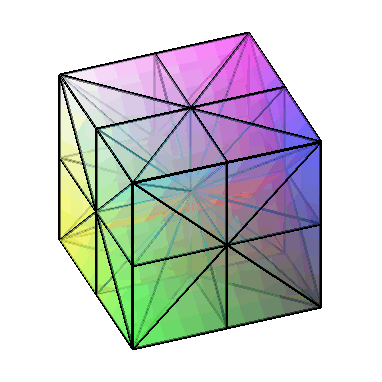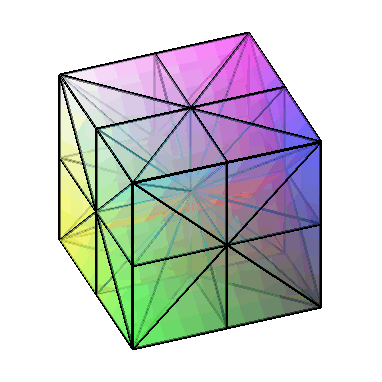
Below we have an image of a cube cut according to the C3 hyperplane arrangement, resulting in 48 cells (= 8 x 6 faces) that correspond to elements of the Weyl group. Another way of thinking about this image is that it is the union of the (closures of) the alcoves neighboring the origin in affine C3. (It is also worth noting that this is the barycentric subdivision of the cube.)
To build the type C3 Steinberg torus, we identify opposite faces of this subdivided polyhedron.